
CAPTAIN Toolbox website
Overview & availability
User interface & examples
Time variable parameter subset
Multivariable transfer function subset
Analysis of advertising data.
Dynamic Linear Regression (DLR) analysis can include harmonic regression and auto-regression as special cases, but here the regressors are specified directly by the user. In this example, we utilise the Captain Toolbox to analyse data representing the success of a particular company's expenditure on advertising. Our model will take the following simple form:
y(t) = a + b . x(t)
where x(t) is the expenditure and y(t) is the response to advertising, where the latter is measured by the company and represented by a number between 0 and 1. The response data contains missing values, represented in Matlab as not-a-number variables and shown as gaps in the graph below.
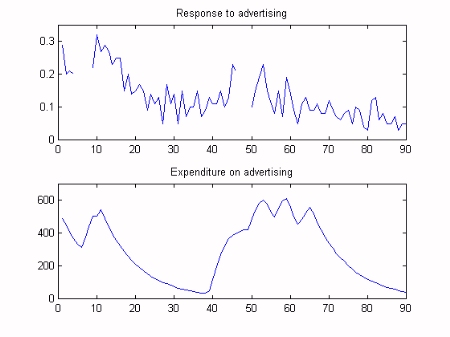
We will assume that the time variable intercept (a) and slope (b) parameters vary in the form of a random walk. The first stage of the analysis is to optimise the Noise Variance Ratio (NVR) hyper-parameters of the model. In the Captain Toolbox, these parameters are optimised via Maximum Likelihood (ML) based on prediction error decomposition. Finally, Kalman Filtering and Fixed Interval Smoothing algorithms are employed to estimate the model, based on the optimsed NVR values. This is achieved with a straightforward call to the Captain Toolbox dlr function. As illustrated in the graphs below, the data lie within the standard error bounds of the smoothed estimates, while the two regression parameters gradually change over time. Note that the algorithms have automatically interpolated over the missing response data.
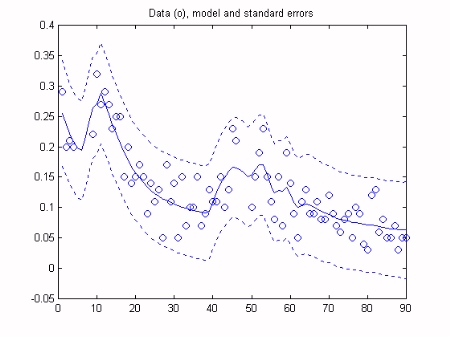
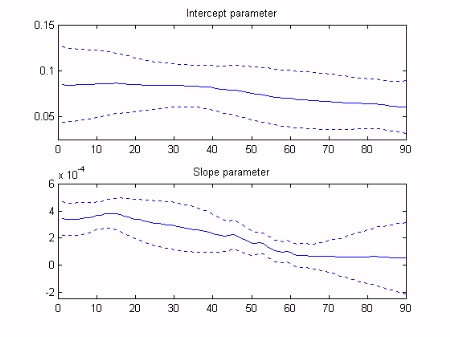
![]()
| previous example | next example |
